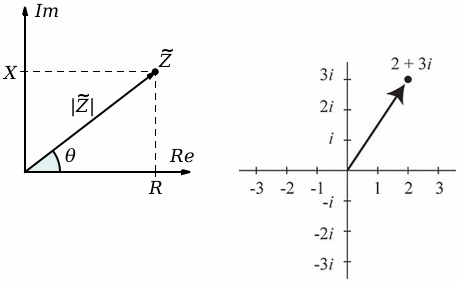
Закон Ома является одной из основных формул в электротехнике и электронике. Он определяет математическую зависимость между электрическим током, напряжением и сопротивлением в электрической цепи. В классической форме закон Ома выражается следующим образом: ток в цепи прямо пропорционален напряжению и обратно пропорционален сопротивлению.
Однако в реальных электрических цепях часто возникают случаи, когда классическая форма закона Ома оказывается неприменимой. При этом применяются комплексные формы закона Ома, которые учитывают влияние таких факторов, как взаимная индуктивность и емкость элементов цепи.
Комплексная форма закона Ома изображается с использованием комплексных чисел и фазовых углов. Возникает комплексное сопротивление, которое состоит из активной части (сопротивление) и реактивной части (индуктивность или емкость). Комплексный ток и напряжение выражаются как действительная и мнимая части комплексных чисел. Фазовый угол между током и напряжением определяет фазовую разность.
Комплексная форма закона Ома широко применяется в решении задач по расчету параметров электрических цепей переменного тока. Она позволяет учесть все взаимодействия элементов цепи и учесть не только активную составляющую, но и реактивную. На практике комплексная форма закона Ома применяется для расчета и проектирования фильтров, трансформаторов, электромоторов и других устройств.
Омов закон: фундаментальный закон электрических цепей
Согласно Омову закону, величина электрического тока (I), протекающего через проводник, прямо пропорциональна напряжению (U), создаваемому в этом проводнике, и обратно пропорциональна сопротивлению (R) этого проводника. Это можно записать следующей формулой:
I = U / R
Это означает, что при постоянном сопротивлении, увеличение напряжения приведет к увеличению силы тока, а при постоянном напряжении, увеличение сопротивления приведет к уменьшению силы тока.
Применение Омова закона широко распространено в электротехнике и электронике. Он используется для рассчета силы тока, напряжения или сопротивления в электрической цепи, а также для определения эффективности и энергопотребления устройств.
Важно отметить, что Омов закон работает только в случае линейности электрической цепи, то есть когда сопротивление не зависит от величины напряжения или силы тока. Для нелинейных цепей, в которых сопротивление изменяется, может потребоваться применение более сложных моделей.
Зависимость силы тока от напряжения и сопротивления
Согласно закону Ома, сила тока в цепи прямо пропорциональна напряжению и обратно пропорциональна сопротивлению:
| Сила тока | Напряжение | Сопротивление |
|---|---|---|
| I | U | R |
| I = U / R | U = I * R | R = U / I |
Из этих формул следует, что чем больше напряжение, тем больше сила тока в цепи. При том же напряжении, чем меньше сопротивление, тем больше сила тока.
Также можно отметить, что при постоянном напряжении, увеличение сопротивления приводит к уменьшению силы тока в цепи. Это объясняется тем, что чем больше сопротивление, тем больше энергии теряется на преодоление этого сопротивления, и меньше энергии остается на протекание тока.
Зависимость силы тока от напряжения и сопротивления имеет множество применений в различных областях, включая электрические цепи, электронику, электротехнику и т.д. Понимание этой зависимости позволяет предсказывать поведение электрических систем и проектировать эффективные схемы и устройства.
Измерение электрической силы тока
Для измерения электрической силы тока в цепи используются специальные приборы, называемые амперметрами. Они могут быть аналоговыми или цифровыми.
Аналоговые амперметры представляют собой стрелочные приборы, в которых сила тока измеряется по углу отклонения стрелки на шкале. Чтение аналоговых амперметров производится путем совмещения конца стрелки с делением на шкале.
Для измерения силы тока в цепи необходимо подключить амперметр включенной цепи параллельно с исследуемым участком, таким образом, чтобы ток проходил через амперметр.
При использовании аналогового амперметра необходимо соблюдать правильную полярность подключения. В случае цифровых амперметров они обычно автоматически определяют полярность тока и позволяют избежать ошибок в измерениях.
| Тип прибора | Преимущества | Недостатки |
|---|---|---|
| Аналоговый амперметр | Простота использования, наглядность | Меньшая точность, влияние сопротивления амперметра на цепь |
| Цифровой амперметр | Высокая точность, автоматическое определение полярности | Высокая стоимость, требует питания |
При измерении электрической силы тока необходимо также учитывать дополнительные факторы, такие как влияние сопротивления проводов и контактного сопротивления. Для получения более точных результатов рекомендуется использовать амперметры с низким внутренним сопротивлением и обеспечить надежное соединение проводов без окисления и перекосов.
Математическая формула закона Ома
Математическая формула закона Ома позволяет описать отношение между напряжением, силой тока и сопротивлением электрической цепи. Исходя из закона Ома, сила тока в электрической цепи пропорциональна напряжению и обратно пропорциональна сопротивлению.
Формула закона Ома записывается следующим образом:
𝑐 = 𝑔 / 𝑢
Где:
- 𝑐 — сила тока (Ампер)
- 𝑔 — напряжение (Вольт)
- 𝑢 — сопротивление (Ом)
Таким образом, с помощью этой формулы можно вычислить силу тока, зная напряжение и сопротивление, а также определить напряжение, зная силу тока и сопротивление в электрической цепи.
Применение закона Ома и его математической формулы особенно важно в электротехнике и электронике при решении различных задач, таких как расчет электрических цепей, определение характеристик компонентов, а также оценка энергопотребления и электрической безопасности систем.
Комплексная форма закона Ома: учет переменного тока
При работе с переменным током, сила тока и напряжение имеют не только амплитудные значения, но и фазовые сдвиги. Для учета этих сдвигов используется комплексная форма закона Ома, которая выражается уравнением Z = V/I, где Z — импеданс, V — комплексное напряжение, I — комплексная сила тока.
Импеданс — это комплексное сопротивление, которое учитывает как активное (сопротивление), так и реактивное (емкостное или индуктивное) сопротивления в цепи. Он выражается как сумма активного и мнимого сопротивления: Z = R + jX, где R — активное сопротивление, X — мнимое сопротивление.
Комплексная форма закона Ома позволяет учитывать фазовые сдвиги и реактивное сопротивление в переменном токе. Она используется при расчете электрических цепей с переменным током, а также при анализе работы различных устройств, таких как фильтры, трансформаторы, генераторы и другие.
| Категория | Формула | Значение |
|---|---|---|
| Сопротивление | R | Активное сопротивление |
| Импеданс | Z | Комплексное сопротивление |
| (Z = R + jX) | X | Мнимое сопротивление |
Таблица представляет основные параметры, используемые в комплексной форме закона Ома при учете переменного тока. Она содержит категории, формулы и их значения. Эти параметры помогают анализировать электрические цепи с переменным током и предсказывать их поведение в различных условиях.
Векторная форма представления переменного тока
Когда речь идет о переменном токе, возникает необходимость в использовании векторной формы представления. Векторная форма позволяет описать переменный ток с помощью двух параметров: амплитуды и фазы.
Амплитуда представляет собой максимальное значение переменного тока и измеряется в амперах. Она указывает на силу переменного тока и определяет его поведение в цепи. Фаза, в свою очередь, отражает смещение переменного тока относительно опорного значения. Фаза измеряется в градусах или радианах и позволяет определить временную задержку между током и напряжением.
Векторная форма представления переменного тока также позволяет учитывать его направление. Вектор тока указывает на амплитуду и фазу и отображается в виде стрелки на комплексной плоскости. Длина стрелки соответствует амплитуде, а угол, под которым она расположена, определяет фазу.
Использование векторной формы представления переменного тока позволяет анализировать его свойства, такие как активная и реактивная мощность, а также проводить расчеты в цепях переменного тока. Это важный инструмент для инженеров и электротехников при проектировании и обслуживании электрических сетей и устройств.
Активная и реактивная составляющие тока
При изучении комплексной формы закона Ома важно понять, что электрический ток может состоять из двух компонент: активной и реактивной составляющих.
Активная составляющая тока представляет собой часть тока, которая используется для переноса энергии и выполнения работы в электрической цепи. Она обусловлена наличием активных сопротивлений, таких как провода, лампочки или нагрузки. Активная составляющая тока измеряется в амперах (А).
Реактивная составляющая тока, с другой стороны, не переносит энергию и не выполняет работы в электрической цепи. Она связана с наличием емкостей, индуктивностей или реакторов в цепи. Реактивная составляющая обусловлена сдвигом во времени между напряжением и током, а ее измеряют в вольтах-амперах-реактивных (вар).
Учитывая активную и реактивную составляющие тока, можно получить полное значение тока через комплексное число, которое называется комплексным током. Он представляет собой векторную сумму активной и реактивной составляющих и измеряется в вольтах-амперах (вар).
Знание активной и реактивной составляющих тока важно для понимания электрических систем и оптимизации их работы. Например, в энергетике реактивная составляющая тока может приводить к потерям энергии и эффективности системы, поэтому ее учет и управление играют важную роль в промышленности и бытовых условиях.
Комплексное сопротивление и его влияние на электрическую цепь
Комплексное сопротивление представляет собой векторную величину, состоящую из активной (действительной) и реактивной (мнимой) частей. Обозначается комплексным числом Z, его модуль называется импедансом и обозначается символом |Z|, а аргумент – фазой сопротивления.
Влияние комплексного сопротивления на электрическую цепь может быть различным в зависимости от его значения. Если комплексное сопротивление равно нулю, цепь является идеальной – в ней нет потерь энергии. Если же комплексное сопротивление имеет только активную (действительную) часть, это означает наличие только активных потерь энергии.
Комплексное сопротивление также может иметь только реактивную (мнимую) часть. В этом случае энергия будет поступать в элемент цепи и затем снова отдаваться ей, без потерь энергии в виде тепла.
Комплексное сопротивление может быть сложной величиной, состоящей как из активного сопротивления, так и реактивного. Это означает, что в цепи происходят и активные потери энергии, и трансфер энергии между элементом и сторонами цепи без потерь. В этом случае комплексное сопротивление будет иметь как активную, так и реактивную части, и его модуль будет больше чем активное сопротивление.
Важно учитывать комплексное сопротивление при проектировании и анализе электрических цепей, так как оно влияет на энергетические потери, передачу энергии и другие характеристики цепи. Используя комплексное сопротивление, можно рассчитать параметры и эффективность цепи, оптимизировать работу устройства и предотвратить несоответствия между теорией и практикой.
Вопрос-ответ:
Что такое комплексная форма закона Ома?
Комплексная форма закона Ома — это математическое выражение, которое связывает напряжение, силу тока и комплексное сопротивление в электрической цепи.
Какие основные принципы лежат в основе комплексной формы закона Ома?
Основные принципы комплексной формы закона Ома основаны на правиле Кирхгофа, которое утверждает, что сумма алгебраических значений токов в узле электрической сети равна нулю, а также на втором законе Кирхгофа, который гласит, что сумма алгебраических значений падений напряжения в замкнутом контуре также равна нулю.
Как применяется комплексная форма закона Ома в реальной жизни?
Комплексная форма закона Ома широко применяется в электротехнике и электронике для анализа и проектирования электрических цепей. Она позволяет рассчитать напряжение, силу тока и сопротивление в различных составляющих цепи, учитывая их взаимодействие и влияние друг на друга.
Какие преимущества имеет использование комплексной формы закона Ома?
Использование комплексной формы закона Ома позволяет более точно и удобно рассчитывать электрические параметры цепей, особенно в случае сложных и нелинейных цепей. Она учитывает фазовые отклонения и реактивные компоненты сопротивления, что позволяет более точно предсказывать поведение электрической цепи.