Формула второго закона Ньютона — основные принципы и примеры расчетов

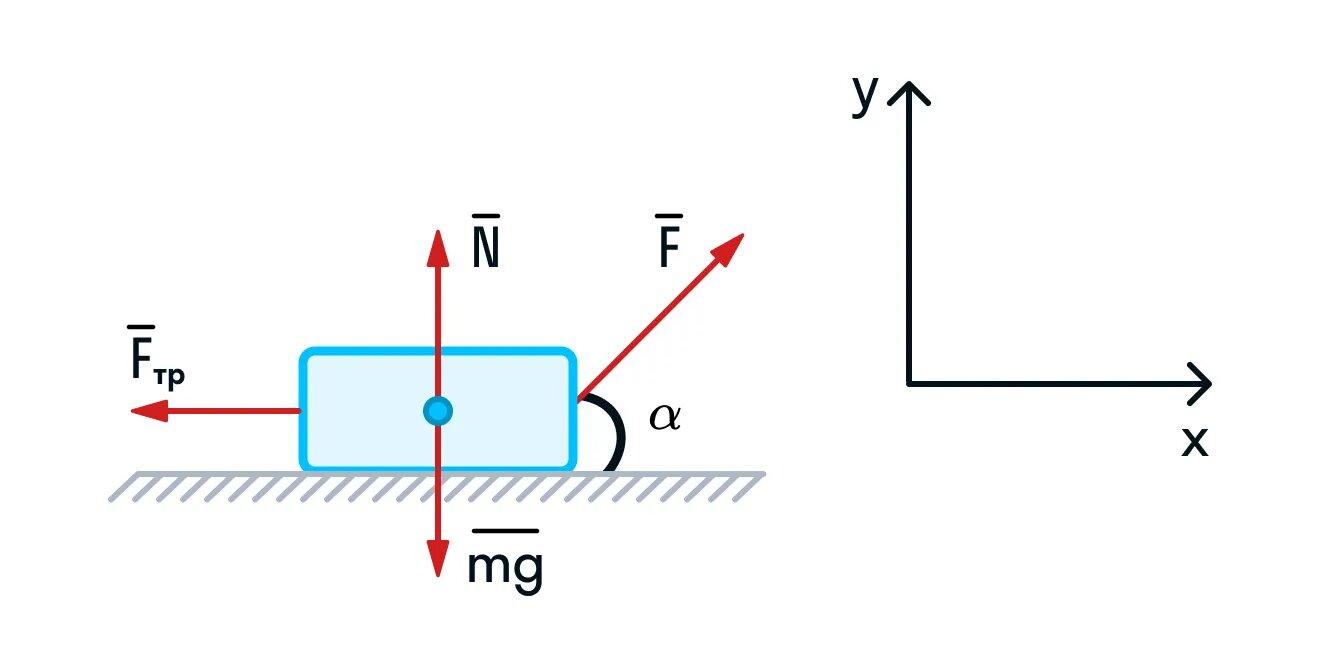
Закон Ньютона – одно из основных положений механики, которое описывает движение объекта под воздействием силы. Формула второго закона Ньютона позволяет рассчитать реакцию тела на действующую на него внешнюю силу и определить величину и направление ускорения. Эта формула является ключевым инструментом для понимания движения объектов и применяется в различных областях науки и техники.

Формула второго закона Ньютона выражается математической записью F = ma, где F – сила, действующая на объект, m – масса объекта, а a – ускорение.

Как следует из этой формулы, сила, действующая на объект, пропорциональна его массе и ускорению. Сила измеряется в ньютонах (Н), масса – в килограммах (кг), а ускорение – в м/с². Используя эту формулу, можно определить силу, которая действует на объект, зная его массу и ускорение, или наоборот – рассчитать ускорение, если известны сила и масса объекта.

Примеры расчетов

Давайте рассмотрим несколько примеров расчета с использованием формулы второго закона Ньютона.

Пример 1:

Пусть у нас есть объект массой 2 кг, на которую действует сила 10 Н. Чтобы найти ускорение этого объекта, мы можем воспользоваться формулой F = ma. Подставляя известные значения, получаем: 10 Н = 2 кг × a. Отсюда выразим ускорение: a = 10 Н / 2 кг = 5 м/с². Таким образом, ускорение объекта равно 5 м/с².

Пример 2:

Представим, что мы знаем массу объекта (5 кг) и его ускорение (3 м/с²), и хотим рассчитать силу, действующую на него. Используя формулу F = ma, получаем: F = 5 кг × 3 м/с² = 15 Н. Таким образом, сила, действующая на объект, равна 15 Н.

Это лишь некоторые примеры применения формулы второго закона Ньютона. Она играет важную роль в физике, инженерии и других областях, где требуется понимание и расчеты движения объектов под воздействием силы.

Принципы второго закона Ньютона

Второй закон Ньютона гласит, что ускорение тела прямо пропорционально силе, действующей на него, и обратно пропорционально его массе. Формула второго закона Ньютона выглядит следующим образом:

F = ma

Где F — сила, m — масса тела, a — ускорение.

Принципы второго закона Ньютона помогают понять фундаментальные законы физики и объяснить множество явлений в механике. Некоторые из ключевых принципов второго закона Ньютона включают:

• Чем больше сила действует на тело, тем больше ускорение оно приобретает.
• Чем меньше масса тела, тем больше ускорение оно получит при действии одинаковой силы.
• Ускорение зависит от направления силы, действующей на тело.
• Действия и реакции равны по величине и противоположны по направлению.

Примеры применения второго закона Ньютона можно найти во многих сферах нашей жизни. Например, при определении траектории полета снарядов, расчете сил, действующих на автомобиль или грузовик при движении, и в множестве других случаев. Расчеты с использованием второго закона Ньютона помогают инженерам и ученым разрабатывать новые технологии и оптимизировать существующие конструкции.

Масса и ускорение

Ускорение, с другой стороны, является мерой изменения скорости тела за единицу времени. Оно обозначается символом «a» и измеряется в метрах в секунду в квадрате. Ускорение может быть положительным или отрицательным, в зависимости от направления движения и действующих сил.

Формула второго закона Ньютона связывает массу, ускорение и силу, действующую на тело. Согласно формуле, сила (F) равна произведению массы (m) на ускорение (a):

F = m * a

Таким образом, если известны масса и ускорение тела, можно рассчитать силу, действующую на него. Эта формула особенно полезна в физике, когда необходимо определить силу, не измеряя ее напрямую.

Например, представим ситуацию, когда тело массой 2 кг движется с ускорением 3 м/с^2. Чтобы рассчитать силу, действующую на это тело, нужно умножить массу на ускорение:

F = 2 кг * 3 м/с^2 = 6 Н

Таким образом, сила, действующая на тело массой 2 кг при ускорении 3 м/с^2, равна 6 Н (ньютонов).

Второй закон Ньютона

Согласно второму закону Ньютона, сила, действующая на тело, пропорциональна ускорению этого тела. Формулировка закона выглядит следующим образом:

Сумма всех сил, действующих на тело, равна произведению массы тела на его ускорение.

Математически второй закон Ньютона записывается в виде:

F = m * a

где F — сила, m — масса тела и a — ускорение.

Данный закон позволяет решать широкий диапазон задач, связанных с движением тел. Например, можно определить силу, необходимую для движения машины определенной массы с заданным ускорением, или рассчитать ускорение тела под действием силы определенной величины.

Важно отметить, что сила в данном законе измеряется в Ньютонах (Н), масса тела — в килограммах (кг), а ускорение — в метрах в секунду в квадрате (м/с^2).

Примеры расчетов с применением формулы

Применение формулы второго закона Ньютона позволяет решать различные задачи, связанные с движением тела под действием силы. Рассмотрим несколько примеров расчетов с использованием данной формулы:

1. Пример 1: Расчет силы тяжести
• Известно, что масса тела равна 5 кг.
• Ускорение свободного падения g принимаем равным 9,8 м/с².
• Используя формулу F = m * g, получаем: F = 5 кг * 9,8 м/с² = 49 Н.
• Таким образом, сила тяжести, действующая на данное тело, равна 49 Н.
2. Пример 2: Расчет силы трения
• Известно, что масса тела равна 10 кг.
• Коэффициент трения между телом и поверхностью равен 0,5.
• Ускорение свободного падения g принимаем равным 9,8 м/с².
• Используя формулу F = μ * m * g, получаем: F = 0,5 * 10 кг * 9,8 м/с² = 49 Н.
• Таким образом, сила трения, действующая на данное тело, равна 49 Н.
3. Пример 3: Расчет силы тяги в наклонном тросе
• Известно, что масса тела равна 2 кг.
• Угол наклона троса к горизонту равен 30°.
• Ускорение свободного падения g принимаем равным 9,8 м/с².
• Используя формулу F = m * g * sin(α), получаем: F = 2 кг * 9,8 м/с² * sin(30°) = 19,6 Н.
• Таким образом, сила тяги в наклонном тросе, действующая на данное тело, равна 19,6 Н.

Приведенные примеры демонстрируют применение формулы второго закона Ньютона для расчета различных сил в физических задачах. Обратите внимание, что для получения верных результатов необходимо использовать единицы измерения в СИ.

Примеры расчетов с применением формулы второго закона Ньютона

Формула второго закона Ньютона (также известный как Закон инерции) позволяет рассчитать величину силы, действующей на тело, и его ускорение. Вот несколько примеров, иллюстрирующих применение этой формулы:

• Пример 1: Рассмотрим движение автомобиля массой 1000 кг, который разгоняется с постоянным ускорением 2 м/с^2. Чтобы найти силу, мы можем использовать формулу F = m * a. Подставив значения по формуле, получим: F = 1000 кг * 2 м/с^2 = 2000 Н. Таким образом, сила, необходимая для разгона автомобиля, равна 2000 Н.

• Пример 2: Рассмотрим тело массой 5 кг, на которое действует сила 10 Н. Чтобы найти ускорение тела, мы можем использовать формулу a = F / m. Подставив значения по формуле, получим: a = 10 Н / 5 кг = 2 м/с^2. Таким образом, ускорение тела равно 2 м/с^2.

• Пример 3: Пусть у нас есть тело массой 2 кг, которое находится на наклонной плоскости. Под действием силы тяжести, тело начинает двигаться с ускорением 4 м/с^2. Чтобы найти силу, действующую по направлению наклона плоскости, мы можем использовать формулу F = m * a. Подставив значения по формуле, получим: F = 2 кг * 4 м/с^2 = 8 Н. Таким образом, сила, действующая на тело, равна 8 Н.

Это лишь некоторые из множества примеров, которые можно рассчитать с помощью формулы второго закона Ньютона. Эта формула позволяет более точно описывать и предсказывать движение тел в различных ситуациях.

Сила трения и ускорение

Второй закон Ньютона гласит, что ускорение тела пропорционально силе, действующей на него, и обратно пропорционально его массе. В математической форме это может быть записано как F = ma, где F — сила, m — масса тела, a — ускорение.

Когда тело движется по горизонтальной поверхности, сила трения может быть рассчитана по формуле f_тр = μN, где f_тр — сила трения, μ — коэффициент трения, N — нормальная сила.

Ускорение тела на горизонтальной поверхности без учета силы трения будет равно a = F/m. Однако, если учитывать силу трения, то ускорение будет меньше, так как сила трения всегда действует против движения и уменьшает скорость тела.

Рассмотрим пример: на горизонтальной поверхности тело массой 5 кг сила трения равна 10 Н, а нормальная сила равна 50 Н. Найдем ускорение этого тела. Используя формулу силы трения f_тр = μN, найдем коэффициент трения, подставим его в формулу ускорения и рассчитаем ускорение по формуле a = (F — f_тр)/m. Полученное значение ускорения будет учитывать и силу трения, и массу тела.

Таким образом, ускорение тела равно 2 м/с².

Гравитационная сила и движение тела

• Пропорциональна произведению масс двух тел, обратно пропорциональна квадрату расстояния между ними.
• Направлена вдоль линии, соединяющей центры масс двух тел.
• Величина гравитационной силы может быть рассчитана с использованием закона всемирного тяготения, сформулированного Исааком Ньютоном.

Для расчета гравитационной силы между двумя телами можно использовать формулу:

G = (G * m1 * m2) / r^2

где G — гравитационная постоянная, m1 и m2 — массы тел, r — расстояние между центрами масс этих тел.

Имея значение гравитационной силы, можно определить ее влияние на движение тела. Согласно второму закону Ньютона, сила, действующая на тело, равна произведению его массы на ускорение, полученное телом под действием силы. Таким образом, гравитационная сила может вызвать ускорение объекта в направлении силы или изменение его скорости и направления движения.

Например, если на тело массой 1 кг действует гравитационная сила, равная 9,8 Н (ускорение свободного падения), то оно будет двигаться вниз с ускорением 9,8 м/с^2. Если же на тело действует гравитационная сила, равная 0 Н, то оно будет находиться в состоянии покоя или двигаться с постоянной скоростью.

Таким образом, гравитационная сила оказывает существенное влияние на движение тела, определяя его траекторию и характер движения.

Вопрос-ответ:

Что такое формула второго закона Ньютона?

Формула второго закона Ньютона описывает связь между силой, массой и ускорением тела. Она гласит, что сила, приложенная к телу, равна произведению массы этого тела на его ускорение. Формально формула записывается как F = m * a, где F — сила, m — масса тела и a — ускорение.

Какими единицами измеряются сила, масса и ускорение в формуле второго закона Ньютона?

Сила измеряется в Ньютонах (Н), масса — в килограммах (кг), а ускорение — в метрах в секунду в квадрате (м/с^2).

Как применить формулу второго закона Ньютона для решения задачи на расчет сил?

Для решения задачи на расчет силы по формуле второго закона Ньютона нужно знать массу тела и его ускорение. Сначала найдем произведение массы на ускорение, затем поделим полученное значение на массу. В итоге получим силу, действующую на тело.

Как применить формулу второго закона Ньютона для решения задачи на расчет массы?

Формула второго закона Ньютона также может быть использована для расчета массы тела. Для этого нужно знать силу и ускорение тела. Сначала выразим массу как отношение силы к ускорению: m = F / a. Затем подставим известные значения и рассчитаем массу тела.

Как формулируется второй закон Ньютона?

Второй закон Ньютона формулируется следующим образом: сила, действующая на тело, равна произведению его массы на ускорение этого тела.

Как можно использовать второй закон Ньютона для расчетов?

Второй закон Ньютона позволяет рассчитывать ускорение тела, если известны масса тела и действующая на него сила. Формула для расчета ускорения выглядит следующим образом: ускорение равно силе, действующей на тело, деленной на массу тела.