Формальная логика — это раздел философии и математики, изучающий формы рассуждений и доказательств. Основным инструментом формальной логики является символика, позволяющая представить логические связи между высказываниями в виде математических символов и формул.
В формальной логике существует ряд законов, которые определяют основные правила преобразования логических формул. Знание этих законов позволяет более точно и логично рассуждать, проводить доказательства и строить аргументацию.
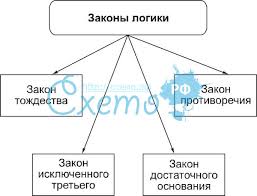
Одним из важнейших законов формальной логики является закон исключения третьего. Он утверждает, что каждое утверждение может быть либо истинным, либо ложным, и не существует третьего состояния. Например, утверждение «Сегодня суббота» может быть либо истинным, либо ложным, нет третьего варианта.
Еще одним примером закона формальной логики является закон двойного отрицания. Он утверждает, что двойное отрицание высказывания равносильно самому высказыванию. Например, высказывание «Не все яблоки красные» равносильно высказыванию «Есть яблоки, которые не красные».
Основные понятия формальной логики
Одно из ключевых понятий формальной логики — это «пропозициональная переменная». Пропозициональная переменная представляет собой символ, который может принимать значение либо истины (true), либо лжи (false). Она используется для задания пропозициональных высказываний, например: «Сегодня солнечно» или «Вода кипит при температуре 100 градусов по Цельсию».
Логическое значение высказывания определяется с помощью операторов логической связки, таких как конъюнкция, дизъюнкция и импликация. Конъюнкция (обозначается символом ∧) обозначает логическое «И». Например, высказывание «Сегодня солнечно ∧ Вода кипит при температуре 100 градусов по Цельсию» будет истинным только в случае, если оба высказывания истинны. Дизъюнкция (обозначается символом ∨) обозначает логическое «ИЛИ». Например, высказывание «Сегодня солнечно ∨ Вода кипит при температуре 100 градусов по Цельсию» будет истинным, если хотя бы одно из высказываний истинно.
Другим важным понятием является «логическое следование» или импликация (обозначается символом →). Импликация задает отношение между двумя высказываниями. Высказывание «Если Сегодня солнечно, то Вода кипит при температуре 100 градусов по Цельсию» будет истинным в случае, если первое высказывание (условие) истинно, либо второе высказывание истинно.
Применение формальной логики в реальной жизни
Еще одной областью, где формальная логика находит применение, является право и юриспруденция. В юридических документах и судебных решениях необходимо строго соблюдать логическую последовательность и правильно анализировать факты и доводы. Формальная логика помогает юристам строить обоснованные доводы и принимать верные решения в сложных правовых ситуациях.
Кроме того, формальная логика широко применяется в информатике и программировании. При разработке программ и алгоритмов важно строить логически правильные структуры и учитывать все возможные варианты развития событий. Формальная логика позволяет программистам достичь максимальной эффективности и надежности своих разработок.
Наконец, формальная логика может быть полезна в повседневной жизни каждого человека. Она помогает нам анализировать информацию, принимать обоснованные решения, развивать критическое мышление и решать проблемы различной сложности. Формальная логика позволяет нам стать более логичными и аналитическими в своем мышлении, что помогает нам эффективно функционировать в современном информационном обществе.
Таким образом, формальная логика имеет широкое применение в реальной жизни и оказывает положительное влияние на различные сферы нашего общества. Понимание основных законов и принципов формальной логики позволяет нам стать более логичными, рациональными и успешными в нашем повседневном и профессиональном общении.
Основные законы формальной логики
| Название закона | Определение | Пример |
|---|---|---|
| Закон исключенного третьего | Любое высказывание либо истинно, либо ложно, без промежуточных значений. | Высказывание «Солнце встает на востоке» истинно, тогда как высказывание «крылья у рыбы» ложно. |
| Закон противоречия | Высказывание не может быть одновременно истинным и ложным. | Высказывание «Сегодня понедельник» не может быть одновременно истинным и ложным. |
| Закон идентичности | Любое высказывание равно самому себе. | Высказывание «Солнце встает на востоке» равно самому себе. |
| Закон исключения третьего | Для любого высказывания, оно либо истинно, либо его отрицание истинно. | Высказывание «Сегодня либо пятница, либо не пятница». |
| Закон двойного отрицания | Двойное отрицание высказывания равно самому высказыванию. | Высказывание «Не правда, что солнце встает на востоке» равно высказыванию «Солнце встает на востоке». |
Законы тождества в формальной логике
Один из основных законов тождества — закон идемпотентности — гласит, что логическое ИЛИ (обозначается символом ∨) и логическое И (обозначается символом ∧) выдают истинное значение, если один из аргументов равен истине. В математической форме этот закон может быть записан следующим образом:
p ∨ p ≡ p
Другой важный закон тождества — закон исключения третьего — гласит, что любое высказывание может быть либо истинным, либо ложным, то есть нет третьего значения. В математической форме этот закон может быть записан следующим образом:
p ∨ ¬p ≡ 1
Закон дистрибутивности — ещё один закон тождества, который определяет отношение между логическим И и ИЛИ. Он позволяет разными способами записывать одно и то же выражение, не изменяя его истинности. В математической форме этот закон может быть записан следующим образом:
p ∧ (q ∨ r) ≡ (p ∧ q) ∨ (p ∧ r)
Законы тождества позволяют упростить логические уравнения и упростить их для анализа и применения в различных областях науки и техники. Понимание и применение законов тождества является важным элементом в формальной логике и позволяет решать сложные задачи с использованием точной логической аргументации.
Законы рассуждений в формальной логике
Применение законов рассуждений позволяет выявлять логические ошибки и противоречия в аргументации, а также анализировать мысли и доводы на предмет их валидности. Законы рассуждений помогают получить более строгие и точные рассуждения, исключая неопределенности и двусмысленности, что особенно важно при проведении научных и логических исследований.
Важно отметить, что формальная логика не ограничивается только математическими рассуждениями. Она применяется во множестве областей, включая философию, искусственный интеллект, право, лингвистику и др. С помощью законов формальной логики возможно анализировать различные языки и рассуждения с точки зрения их логической структуры.
Примеры законов рассуждений в формальной логике:
- Закон исключённого третьего: каждое утверждение должно быть либо истинным, либо ложным, без третьего варианта;
- Закон противоречия: невозможно, чтобы одновременно истинно было утверждение и его отрицание;
- Закон двойного отрицания: двойное отрицание любого утверждения равно самому этому утверждению;
- Закон де Моргана: отрицание конъюнкции равно дизъюнкции отрицаний, и наоборот;
- Закон импликации: если утверждение p следует из утверждения q, толко если отрицание p противоречит утверждению q.
Знание и применение законов рассуждений в формальной логике является важной компетенцией при построении логически согласованных доводов и аргументаций.
Законы равенства в формальной логике
Законы равенства позволяют сравнивать значения, утверждать их равенство или неравенство. Некоторые из основных законов равенства в формальной логике:
- Закон рефлексивности: a = a
- Закон симметричности: Если a = b, то b = a
- Закон транзитивности: Если a = b и b = c, то a = c
- Закон замены: Если a = b, то a можно заменить на b в любом выражении
- Закон совместимости: Если a = b, то a можно заменить на b и наоборот
Эти законы равенства позволяют строить цепочки рассуждений и уравнений, которые могут быть использованы для доказательства или опровержения различных утверждений в формальной логике.
Применение законов равенства в формальной логике может быть полезно при решении задач из различных областей, таких как математика, философия, информатика и другие. Знание этих законов и умение правильно их использовать является важным навыком для успешного решения логических задач.
Примеры применения формальной логики
Формальная логика широко применяется в различных областях науки и ежедневной жизни.
В философии формальная логика позволяет анализировать и выстраивать сильные аргументы, строить логические цепочки рассуждений и опровергать некорректные умозаключения. Она позволяет точно определить условия и предпосылки, а также идентифицировать ошибки в мышлении. Формальная логика помогает философам разрабатывать системы аксиом и формулировать логические законы, которые используются в различных философических дисциплинах.
В информатике формальная логика играет важную роль в разработке программного обеспечения и алгоритмов. Она позволяет точно описывать логические и условные операторы для управления поведением компьютерных программ. Формальная логика используется для проверки и верификации программ, устранения ошибок и улучшения их производительности. Она также применяется в компьютерных науках для разработки новых моделей вычислений и алгоритмов.
В ежедневной жизни формальная логика помогает нам анализировать и принимать решения, строить логические цепочки аргументации и избегать ошибок мышления. Она помогает нам структурировать информацию, анализировать доказательства и верифицировать утверждения. Формальная логика является неотъемлемой частью критического мышления и позволяет нам развивать логическую грамотность и качественно мыслить.
Применение формальной логики в математике
Основные законы формальной логики, такие как законы классического исчисления высказываний и квантора всеобщности, позволяют нам строить математические доказательства с помощью аккуратно структурированных логических шагов.
Применение формальной логики в математике не только облегчает процесс доказательства, но и позволяет устанавливать связи между разными разделами математики. Логические операции, такие как конъюнкция, дизъюнкция, импликация и отрицание, позволяют нам изучать логические свойства математических объектов.
Например, применение формальной логики в теории множеств позволяет доказывать теоремы о включении множеств, пересечении, объединении и разности. Также она играет важную роль в алгебре, где законы формальной логики используются для доказательства свойств операций над алгебраическими структурами.
Применение формальной логики в политике
Одним из основных применений формальной логики в политике является анализ публичных высказываний политических деятелей. Посредством логической дедукции и рассуждений можно выявить аргументационные противоречия, логические ошибки и нелогичные утверждения, что позволяет потенциально опровергнуть или подтвердить их рациональность.
Другим сложным вопросом в политике является обработка больших объемов данных. При принятии решений политики часто сталкиваются с проблемой анализа и обработки огромных массивов информации. Формальная логика предоставляет инструменты для приемлемого и точного представления данных, их систематизации и анализа, что позволяет принимать эффективные решения на основе надежной информации.
Наконец, формальная логика может быть полезна при принятии решений в сложных политических ситуациях. Путем анализа разных факторов и применения логических правил можно провести аргументацию в пользу той или иной стратегии, определить наиболее целесообразные действия и предсказать возможные последствия. Это особенно актуально в условиях неопределенности и разнообразных интересов.
В итоге, применение формальной логики в политике позволяет политическим деятелям разрабатывать обоснованные стратегии, делать информированные решения, а также убедительно аргументировать свои позиции. Она является мощным инструментом для критического мышления и анализа, что делает ее неотъемлемой частью политического процесса.
Вопрос-ответ:
Что такое формальная логика и какие законы она предполагает?
Формальная логика — это раздел философии и математики, изучающий правила и законы рассуждений и выводов. Основные законы формальной логики включают в себя законы исчисления высказываний, законы равносильности и законы преобразования высказываний.
Какие примеры применения формальной логики есть в повседневной жизни?
Примеры применения формальной логики в повседневной жизни можно найти в решении логических головоломок, в обосновании аргументов в дебатах, в принятии рациональных решений и в построении логических цепочек рассуждений.
Чем отличается формальная логика от интуитивной?
В отличие от интуитивной логики, которая основана на интуиции и личных предположениях, формальная логика стремится установить строгое формальное описание правил рассуждений и выводов. Формальная логика полагается на логические законы и предоставляет возможность проверять корректность рассуждений.
Какие законы преобразования высказываний используются в формальной логике?
Законы преобразования высказываний в формальной логике включают законы дистрибутивности, законы поглощения, законы двойного отрицания и законы де Моргана. Эти законы позволяют преобразовывать и упрощать выражения, сохраняя их истинностное значение.